Avec formalisme SWAT

Définition

Voir la description du modèle hydrologique générique.

Le modèle SWAT est un modèle à l’échelle d’un bassin versant, qui modélise non seulement le cycle d’eau fluvial (phase routage), mais aussi le cycle d’eau sur terre (phase sol)

Il est basé sur une description physique réaliste des processus en jeu. Le niveau d’abstraction dans SWAT est donc moins élevé que dans les modèles conceptuels. Même s’il est bien plus riche (en nombre d’équations et de variables), SWAT est plus immédiat à appréhender, car il propose une modélisation très descriptive et fidèle de la dynamique d’un bassin-versant.

SWAT intègre des processus modélisant les pressions anthropiques sur l’eau, notamment les activités agricoles, ces processus étant déjà intégrés dans Maelia ils ne sont pas considérés.

Il s’agit d’un modèle semi-empirique utilisé et soutenu par une im- portante communauté scientifique (plus de deux mille utilisateurs), et la plupart des équations ont été calibrées sur de nombreux bassins- versants du monde.  Enfin, SWAT peut être utilisé pour calculer des teneurs en sédiments et nutriments, telles que les pesticides dans l’eau. Intégrer une réflexion 
 sur la qualité de l’eau fait partie des perspectives de développement futur du projet Maelia.

Description

Le modèle hydrologique basé sur les formalismes SWAT peut se découper en deux grandes phases :

Avant de pouvoir effectuer les analyses et calculs des processus physiques du cycle de l’eau, certaines caractéristiques géographiques et hydrologiques du B.V. doivent être calculées à partir des données du MNT. Celles-ci incluent les temps de concentration pour les BVe, les temps de latence des surface runoff (time-lag), les durées nécessaires aux lateral flow pour atteindre le cour d’eau principal, etc. Les variables définies au niveau de chaque BVe sont marquées avec un (i), représentant le ième BVe. Celles définies au niveau d’une HRU ainsi qu’au niveau de la Bande d’élévation[?] sont indexées avec un (j) ou (ib), représentant la jeme HRU ou la ibeme bande d’un BVe donnée. Enfin, les variables définies au niveau d’une couche du sol[?] sont indexées avec un (jj), représentant la jjeme couche du sol d’une HRU donnée.

Les processus phase sol et phase routage sont organisés en plusieurs sections, chaque section représentant un sous-ensemble des phénomènes simulés par notre implémentation de SWAT. Pour une meilleure compréhension du modèle, et pour marquer une distinction claire entre les variables qui sont à nourrir par des données provenant du terrain, et celles dont il faudra caler la va- leur par ajustements successifs afin de reproduire finement les débits, notre présentation des variables du modèle est structurée comme suit :

Variables d’entrée

Ce sont les variables dont la valeur est définie par l’utilisateur. Il s’agit donc soit de données ”d’entrée”, soit des paramètres.

Variables de sortie

Variables de sortie : Les variables qui vont être enregistrées dans un fichier à la fin de la simulation et observées. Un sous-ensemble de celles- ci correspondent aux indicateurs qui vont permettre d’évaluer chaque scénario simulé.

Variables intermédiaires

Ce sont des variables qui sont calculées par des processus du modèle puis utilisées par d’autres processus, intervenant séquentiellement plus tard dans la simulation.

Variables locales

Les variables nécessaires localement pour certains processus dans une section.

Calcul des temps de concentration

Remarque : Les algorithmes 1.1.1 – 1.1.3 sont basés sur le fichier ”hydroinit.f” des codes source du modèle SWAT et le chapitre 2 :1.3 de la documentation théorique (2009).

Variables d’entrée

↓ LChTri(i) : La longueur du cours d’eau tributaire qui ”s’écoule” à partir du point le plus éloigné de l’exutoire dans un BVe (km) ;

↓ Lslp,zh(i) : La longueur moyenne de la pente pour le BVe (m), Lslp,zh = 50 par défaut, on pourra l’utiliser pour tous les BVe ;

↓ slpChTri(i) : La pente moyenne pour le cours d’eau tributaire (m/m);

↓ slphru(i) : La pente terrestre moyenne pour toutes les HRUs dans un BVe donnée (m/m) ;

↓ nChTri(i) : La valeur du coefficient de Manning pour le cours d’eau tributaire ;

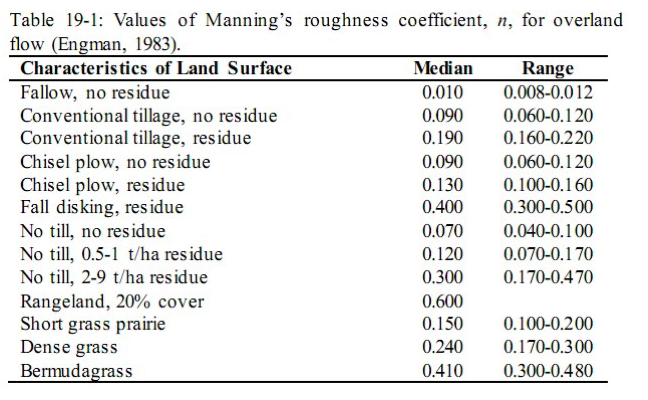
↓ nterrain(i) : La valeur du coefficient de Manning pour les flux sur terrain (i.e. surface runoff), NB : les valeurs habituellement utilisées par les utili- sateurs de SWAT pour nterrain et nChTri sont listés dans les tableaux de la documentation théorique de SWAT ;

↓ AreaBV : La Superficie du Bassin-Versant (km2) ;

↓ Frhru,BV (j) : La fraction du B.V. qui est contenue dans la HRU d’indice j (km2/km2) ;

↓ F rzh,BV (j) : La fraction du B.V. qui est contenue dans le BVe d’indice i (km2/km2) ;

↓ ZHhru(i) : Le BVe dans lequelle se trouve la HRU d’indice j ;

↓ surlag : La valeur du coefficient du surface runoff lag (exprimée en jour). Il s’agit d’un paramètre qui doit être calibré. Par défaut, surlag = 4, valeur calibrée au cours des projets de l’Ecolab lors des applications de SWAT sur des sous-parties du BAG : surlag = 0.9 ;

Variables intermédiaires

↑ tczh(i) : Le temps de concentration pour le BVe d’indice i. (hr) ;

↑ tconc(j) : Le temps de concentration pour la HRU d’indice j. (hr) ;

↑ brt(j) : La fraction du surface runoff qui arrive dans le cours d’eau du BVe dans le courant de la journée ;

Variables locales

tterrain(i) : Durée d’écoulement des flux vers le cours d’eau tributaire.(hr)

tChT ri(i) : Durée de trajet pour le cours d’eau tributaire (hr) ;

Calcul des temps de concentration pour les Bve

\begin{algorithm} \caption{Algorithme 1.1.1} $t_{terrain}=\displaystyle\frac{L_{slp,zh}\ ^{0.6}\ *\ n_{terrain}\ ^{0.6}}{18\ *\ slp_{hru}^{0.3}}$;\\ \vspace{1em} $t_{ChTri}=\displaystyle\frac{0.62\ *\ L_{ChTri}\ *\ n_{ChTri}\ ^{0.75}}{(Area_{BV}*Fr_{zh,BV}(ZH_{hru}))^{0.125}\ *\ slp_{ChTri}\ ^{0.375}}$;\\ \vspace{1em} $tc_{zh}(ZH_{hru})= t_{terrain}+t_{ChTri}$;\\ \end{algorithm}

Calcul des temps de concentration pour les HRUs

Remarque : On peut calculer le temps de concentration indépendamment pour chaque HRU. Les équations pour calculer tconc et tczh sont identiques, la seule différence réside dans le calcul de tChT ri : lors du calcul de tconc, il est considéré que le cours d’eau tributaire dans un BVe est assigné entre les différentes HRU en tenant compte du proportionnellement du BVe en HRU, la superficie de chaque HRU peut être aussi calculée.

\begin{algorithm} \caption{Algorithme 1.1.2} $L_{ChTri}(j)=L_{ChTri}(i)*\displaystyle\frac{Fr_{hru,BV}(i,j)}{Fr_{zh,BV}(i,ZH_{hru})}$;\\ \vspace{1em} $t_{terrain}(j)=\displaystyle\frac{L_{slp,zh}\ ^{0.6}\ *\ n_{terrain}\ ^{0.6}}{18\ *\ slp_{hru}^{0.3}}$;\\ \vspace{1em} $t_{ChTri}=\displaystyle\frac{0.62\ *\ L_{ChTri}\ *\ n_{ChTri}\ ^{0.75}}{(Area_{BV}*Fr_{hru,BV})^{0.125}\ *\ slp_{ChTri}\ ^{0.375}}$;\\ \vspace{1em} $t_{conc}(j)= t_{terrain}(j)+t_{ChTri}$;\\ \end{algorithm}

Calcul de la fraction du surface runoff qui peut arriver au cours d’eau lors de la journée

\begin{algorithm}[H] \caption{Algorithme 1.1.3} $brt=1-exp(\displaystyle\frac{-surlag}{t_{conc}})$; \end{algorithm}

Calcul des durées de trajet pour les lateral flows

Remarque : L’algorithme 1.2 est basé sur le fichier ”hydroinit.f” des codes source du modèle SWAT et le chapitre 2 :3.5 de la documentation théorique (2009).

Variables d’entrée

↓ Lslp,sol(j) : la longueur moyenne de la pente à parcourir pour les lateral flows (m), elle vaut par défaut Lslp,zh = Lslp,sol = 50 ; on pourra utiliser cette valeur pour toutes les BVe ;

↓ Ksat(jj, j) : conductivité hydraulique saturée (mm/hr) du sol

↓ tilelag : en cas de drainage, cette variable indique le délai ajouté par les tuyaux de drainage (hrs) ;

Variables intermédiaires

TTlag(j) : La durée du trajet pour le lateral flow(days) par défaut, il estégal à 0. Cette valeur peut être calculée par le modèle, ou traitée comme un paramètre.

↑ Frttlag(j) : La fraction du lateral flow qui peut arriver au cours d’eau au cours de la journée ;

Variables locales

Ksat,mx(j) : La conductivité hydraulique maximale à saturation pour une HRU (mm/hr)

\begin{algorithm} \caption{Algorithme 1.2} $tile_{lag}\ ?\;\ TT_{lag}=\displaystyle\frac{tile_{lag}}{24};\ \mid\ \rightarrow$ \scriptsize $\backslash\backslash$ La duree du trajet peut etre calculee a partir des donnees d'entree du drainage. \\ \normalsize \vspace{1em} $TT_{lag}\geq 0\ ?;\ \rightarrow;\ \mid$ \scriptsize $\backslash\backslash$ S'il n'y a pas de donnée d'entrée mesurant le drainage, on peut le calculer a partir de la conductivite du sol \\ \normalsize \vspace{1em} $K_{sat,mx}(j)=Max(K_{sat}(jj,j));$ \scriptsize $\backslash\backslash$ NB : il est necessaire de comparer les conductivites de toutes les couches du sol pour trouver le $K_{sat,mx}$ de chacune des HRU \\ \normalsize \vspace{1em} $TT_{lag}=10.4*\displaystyle\frac{L_{slp,hru}}{K_{sat,mx}}$. \\ \vspace{1em} $Fr_{ttlag}=1-exp(\displaystyle\frac{-1}{TT_{lag}})$;\\ \end{algorithm}

Calcul des coefficients associés au routage de l’eau dans les cours d’eau

Remarque : L’algorithme 1.3.1 – 1.3.4 sont basés sur les fichiers ”qman.f” et ”ttcoef.f” des codes source du modèle SWAT et le chapitre 7 :1.1, 7 :1.2 et 7 :1.4 de la documentation théorique (2009).

Le modèle SWAT fait l’approximation que le cours d’eau principal d’un bassin versant est de forme trapézoïdale.

La forme trapézoïdale des cours d’eau.
La forme trapézoïdale des cours d’eau.
Variables d’entrée

↓ LCh(i) : La longueur du cours d’eau dans le BVe i (km) ;

↓ Wbnkful(i) : La largeur moyenne à la surface (au miroir) des cours d’eau dans un BVe (m) ;

↓ depthbnkful(i) : La profondeur moyenne au miroir du cours d’eau du BVe i (m);

↓ slpch(i) : La pente moyenne du cours d’eau dans le BVe i (m/m) ;

↓ nCh(i) : La valeur du coefficient de Manning pour le cours d’eau ; par défaut nCh = 0.1

↓ zch(i) : La pente du côté du cours d’eau (m/m) ; par défaut zch = 2

Variables intermédiaires

↑ Abnkful(i) : Superficie de la section mouillée au miroir des cours d’eau (m2);

↑ Wbtm(i) : La pente du coté du cours d’eau (m/m) ;

↑ qbankful(i) : Le débit du cours d’eau au miroir (m3/s);

↑ Kch,bnkful(i) : Le ratio de stockage à débit pour un cours d’eau miroir (hr);

↑ Kch,0.1 bnkful(i) : Le ratio de stockage à débit pour un cours d’eau lors du 0.1 de profondeur de miroir (bnkful) (hr);

Variables locales

P (i) : La périmètre mouillé (m) ;

R(i) : Le rayon du cours d’eau (m) ;

Ck(i) : La wave celerity (m/s);

ν(i) : La vitesse moyenne des flux (m/s);

Fonction externe : Fonction real Qman(x1, x2, x3, x4)

L’équation de Manning pour calculer la vitesse du cours d’eau et le débit va être utilisée plusieurs fois : pour calculer les coefficients de cours d’eau et également dans la phase de routage. Il est pratique de la définir comme une fonction externe :

x1, (m2) ou none : Egale soit à la superficie de la section mouillée, soit à 1. Quand elle estégale à 1, la fonction va calculer la vitesse de l’eau. Si x1 = A, alors c’est le débit qui est calculé.

x2, (m) : Le rayon hydraulique (P )

x3 : La valeur du coefficient de Manning pour le cours d’eau considéré (nCh)

x4, (m/m) : La pente moyenne du cours d’eau (slpch)

\begin{algorithm} \caption{Algorithme 1.3.1} $qman=0;$\\ $qman=\displaystyle\frac{x1*x2^{0.6666}*sqrt{x4}}{x3}$\\ \scriptsize $\backslash\backslash$ $qman$ est la valeur de sortie de cette equation (exprimee en $m^3/s$ ou $m/s$ selon la valeur de $x1$). \normalsize \end{algorithm}

Calcul de la largeur du fond du cours d’eau

\begin{algorithm} \caption{Algorithme 1.3.2} $W_{btm}=W_{bnkful}-2*Z_{ch}*\textit{depth}_{bnkful};$\\ $W_{btm}>0?,\ \rightarrow; \vert \ \ W_{btm}=0.5*W_{bnkfull}, Z_{ch}=\frac{W_{bnkfull} - W_{btm}}{2* \textit{depth}_{bnkfull}}; \textit{finsi}; $\\ \scriptsize $\backslash\backslash$ Verifier si le $W_{btm}>0$,(si $W_{btm}<0, Z_{ch}\neq 2$). \normalsize \end{algorithm}

Calcul de A, P, et Q pour le cours d’eau au miroir

\begin{algorithm} \caption{Algorithme 1.3.3} $A_{bnkful}=(W_{btm}+Z_{ch}*\textit{depth}_{bnkful})*\textit{depth}_{bnkful};$ \\ \vspace{0.5em} $P_{bnkful}=W_{btm}+2*\textit{depth}_{bnkful}*\sqrt{1+Z_{ch}^2};$ \\ \vspace{0.5em} $R_{bnkful}=\frac{A_{bnkful}}{P_{bnkful}}; $\\ \vspace{0.5em} $q_{bnkful}=Qman(A_{bnkful},R_{bnkful},n_{Ch},slp_{ch});$\\ \vspace{0.5em} $\nu_{bnkful}=Qman(1,R_{bnkful},n_{Ch},slp_{ch});$\\ \vspace{0.5em} $C_{k,bnkful}=\displaystyle\frac{\nu_{bnkful}*5}{3};$\\ \vspace{0.5em} $K_{ch,bnkful}=\displaystyle\frac{L_{ch}}{3.6*C_{k,bnkful}*5};$\\ \end{algorithm}

Calcul de A, P , K et q, lorsque la profondeur du cours d’eau est égal à un dixième de la surface au miroir

\begin{algorithm} \caption{Algorithme 1.3.4} $d=0.1*\textit{depth}_{bnkful};\ A_{0.1bnkful}=(W_{btm}+Z_{ch}*d)*d;$ \\ \vspace{0.5em} $P_{0.1bnkful}=W_{btm}+2*d*\sqrt{1+Z_{ch}^2};$ \\ \vspace{0.5em} $R_{0.1bnkful}=\frac{A_{0.1bnkful}}{P_{0.1bnkful}}; $\\ \vspace{0.5em} $q_{0.1bnkful}=Qman(A_{0.1bnkful},R_{0.1bnkful},n_{Ch},slp_{ch});$\\ \vspace{0.5em} $\nu_{0.1bnkful}=Qman(1,R_{0.1bnkful},n_{Ch},slp_{ch});$\\ \vspace{0.5em} $C_{k,0.1bnkful}=\displaystyle\frac{\nu_{0.1bnkful}*5}{3};$\\ \vspace{0.5em} $K_{ch,0.1bnkful}=\displaystyle\frac{L_{ch}}{3.6*C_{k,0.1bnkful}*5};$ \end{algorithm}

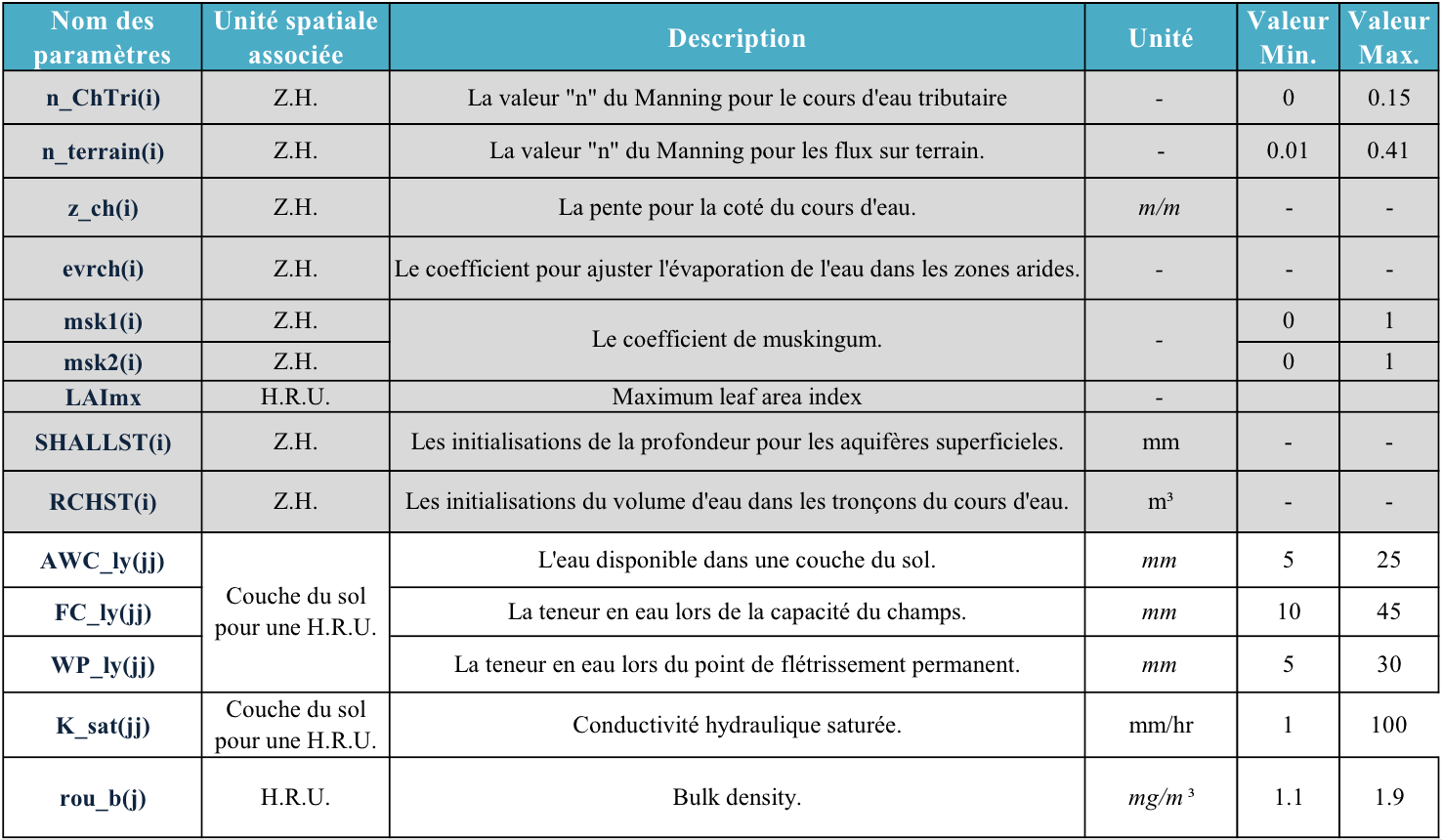
Paramètres calibrés

  • nChTri(i) : La valeur ”n” du Manning pour le cours d’eau tributaire, il vaut 0.1 par défaut

    lkjjà
    nChTri(i)
  • nterrain(i) :La valeur ”n” du Manning pour les flux sur terrain (surface ru- noff ), il vaut 0.35 par défaut

    nTerrain
    nTerrain
  • surlag : coefficient de surface runoff lag (days), c’est un paramètre important, on va le calibrer. par défaut, surlag = 4.
  • nCh(i) : La valeur ”n” du Manning pour le cours d’eau ; nCh = 0.1 par défaut

    nCh(i)
    nCh(i)
  • zch(i) : La pente pour la coˆté du cours d’eau (m/m) ; zch = 2 par défaut, on pourra l’utiliser comme une constante
  • CN2(j) : Condition moite II, dans un premier temps, on va utiliser les va- leurs calibrées par l’Ecolab, AGRL : 80, FRST : 70, URBN 65
  • ρb(j) : Bulk density (mg m−3), c’est le rapport de la masse de particules solides sur le volume total du sol. MS / VT , masse des solides / volume total ; ρb <0?ρb =1.3; ρb >2?ρb =2;cettevaleurestentre(1.1-1.9)
  • ESCO(j) : Coefficient de compensation entre les différentes couche du sol lors des calculs d’évaporation du sol.
Ce coefficient nous permet de modifier la distribution de la demandeévaporative pour les différentes couches du sol. ESCO doit être entre (0.01, 1),plus la valeur est basse, plus le modèle est capable d’extraire de l’eau par évaporation dans les couches inférieurs du sol.

    ?
    ?
  • EPCO(j) : Coefficient de compensation entre les différentes couche du sol lors des calculs de la transpiration des plantes.
Quand il n’y a pas assez de l’eau dans les couches supérieures, ce fac- teur nous permet de utiliser l’eau des couches inférieures du modèle. EPCO doit être entre (0.01, 1).
  • δgw(j) : Temps entre l’eau sortant du profil du sol et entrant dans la shallow aquifère (days). (Le temps s’écoulant dans la zone vadose).
  • αgw(j) : Base flow récession constant. L’indice des flux sous-terrains pour répondre aux changements des recharges.
  • βrev(j) : ”revap” coefficient pour l’eau sous-terrain.(0.02-0.2).
  • βdeep(j) : Le coefficient de percolation vers l’aquifère profond.
  • evrch(i) : Le coefficient pour ajuster l’évaporation de l’eau dans les zones arides, evrch = 1 pour nous normalement
  • msk1(i), msk2(i) : Le coefficient de muskingum pour calculer le Kmsk(i), le storage time constant, (msk1 + msk2 = 1).
  • mskX(i) : Le coefficient de muskingum représentant la cheville, cette valeur est entre (0 – 0.5), il vaut 0.2 par défaut
  • SHALLST,DEEPST,GWHT :Initialisationpourlaprofondeurdeshal- low/deep aquifère (mm) ; et la hauteur de l’eau souterraine (m)
  • aqshthr,q(j) : La limite (Threshold) de l’eau dans l’aquifère superficiel pour le base flow (mm)
  • aqshthr,rev(j) : La limite du niveau d’eau pour ”revap” dans l’aquifère super- ficielle (mm)
  • tlaps(i) : L’augmentation de la température par rapport l’augmentation de l’altitude, ◦C/km(i). Cette valeur pourra être négative.
  • plaps(i) : L’augmentation de la précipitation par rapport l’augmentation de l’altitude, mm/km(i).
  • sftmp, smtmp (i) : snow-fall temperature (chute de neige) et snow-melt temperature (fond de neige) (◦C) pour un BVe. On pourra définir des valeurs de ces deux paramètres pour tout les BVe.
  • smf mn, smf mx (i) : minimum snow-melt rate (21 Dec.) et maximum snow- melt rate (21 Jun.) (mm/◦C/day) pour un BVe. Ici le ◦C est la température de l’air. Ces deux paramètres permettent que le taux de fonte de neige varie pendant une année. Les valeurs de ces deux paramètres dépendent des impacts de la température du sol sur la fonte de neige.
  • snocovmx, sno50cov (i) : Teneur minimale en eau du paquet de neige qui correspond à la couverture 100% de neige(mm) ; Fraction de snocovmx qui correspond à la couverture 50% de neige(none).
  • timp(i) : Le facteur de lag pour le paquet de neige(none). Il contrôle les influences de la température du paquet de neige du jour précédent. Sa valeur est entre (0.01 – 1).

Paramètres sensible (Pour qui les calibrages sont obligatoires)

Nom des paramètres Unité spatiale associée Description Unité Min. Valeur Max. Valeur Calibrée SWAT
ESCO(j) H.R.U. Factuer de compensation pour l’évaporation du sol – 0 1 1
EPCO(j) H.R.U. Factuer de compensation pour la transpiration de la plant – 0 1 0.3
Surlag(j) H.R.U. Coefficient du temps de retard pour le surface runoff Jours 0 10 4
Delta_gw(j) H.R.U. Le temps retard pour l’eau souterrain. (La durée du trajet dans la zone vadose) Jours 0 500 31
beta_rev(j) H.R.U. Le coefficient « revap » pour l’eau souterrain. – 0.02 0.2 0.01
beta_deep(j) H.R.U. Le coefficient de percolation ves l’aquifère profond. – 0 1 0.05
alpha_gw(j) H.R.U. L’index des flux sous-terrain pour répondre aux changements des recharges. – 0 1 0.01
aq_shthr,rev(j) H.R.U. La limite de l’eau pour « revap » dans l’aquifère superficiele. mm 1500
aq_shthr,q(j) H.R.U. La limite de l’eau pour le « base flow » dans l’aquifère superficiele. mm 0
AGRL: 75
CN_2(j) H.R.U. SCS Curve number (Comme les pentes sont > 5% par tout, on a activé l’option d’ajuster le CN2 avec la pente dans SWAT, si on veut le simuler dans MAELIA, voir l’algo. 14 dans la documentation Hydrologique MAELIA) – 35 98 FRST: 70
URBN: 65
WATR: 92
n_ch(i) Z.H. La valeur « n » du Manning pour le cours d’eau. – 0 0.15 0.014

 

Paramètres Neige (Pour les prochaines étapes)

sftmp Z.H. Snow-fall temperature °C 0.025
smtmp Z.H. snow-melt temperature °C 0.01
smfmn Z.H. minimum snow-melt rate (21 Dec.) mm/°C/day 0.025
smfmx Z.H. Maximum snow-melt rate (21 Jun.) mm/°C/day 0.025
snocovmx Z.H. teneur minimale en eau du paquet de neige qui correspond à la couverture 100% de neige mm 0.01
sno50cov Z.H. Fraction de snocovmx qui correspond à la couverture 50% de neige – 0.025
timp Z.H. Le lag facteur pour le paquet de neige – 0.025
PLAPS Z.H. L’augmentation de la précipitation par rapport l’augmenttation de l’altitude mm/km/year –
TLAPS Z.H. L’augmentation de la température par rapport l’augmenttation de l’altitude °C/km/year –
SNO_SUB Z.H. L’inistialisation de neige dans le paquet de neige mm –

 

Image processus_swat_general
Paramètres insensible (Pour qui les calibrages ne sont pas obligatoires)

Références